Method for the estimation of Process Capability when sample size is less than 30

Summary

The use of capability indexes or metrics is vital in industry. It allows engineers to predict how the
process is going to behave in terms of the ability to meet costumer’s expectations. There are some rules to determine the appropriate sample size to estimate process capability with the highest precision that is possible. For instance, the most well-known rule is the one that estates the minimum sample size should be 30 individual measures. Sometimes, due to different reasons, such as lack of time, budget, etc., engineers cannot afford 30 units/measures for their capability studies.
Ignoring this fact and assuming that the traditional formulae for Cpk estimation is still applicable
when having less than 30 observations is a mistake. This document explains a method to estimate process capability with less than 30 measures without disregarding estimation uncertainty. It is developed using two different approaches. The first one presents the worst case, which is the lower bound, and the second one extends it to estimate the whole confidence interval, lower and upper bound for a given α.

1 Introduction and method fundamentals

The rule of 30 units as the minimum sample size for capability estimation is coming from one of
the consequences of the Central Limit Theorem (CLT), which is:

It means that if we have a random variable with a certain probability distribution and we estimate
its standard deviation, the standard deviation of the mean, when we take several observations
instead of individuals, will be the standard deviation of the individual observations divided by the
square root of the sample size (n).
If we draw the function of 1/√n in a chart the result is shown in the figure 1:

In figure one, we can see why the rule of 30 units as minimum is used. With 30 units the variability of the mean is almost converging and is quite far away from the “elbow” of the chart.

Nevertheless, it depends on the precision we want for our parameter estimation. One can argue
that until about 200 units we do not see how the asymptotic function is converging into an almost
parallel function to the horizontal axis. In general, we can also say that the improvement we get
from increasing sample size from 30 to 200 units is not so much if we compare it to the difference
when we are moving in the other direction, that is, when we decrease the sample size, since we
get close to the “elbow” of the chart very rapidly.
We can think that by fulfilling the rule of not estimating process capability with less than 30 units
is enough. But, in many cases, having 30 units is a not affordable luxury or it is just not possible for other reasons. If one remembers, the expression for Cpk estimation is:

Where USL and LSL are the Upper Specification Limit and Lower Specification Limit of the
characteristic we are estimating its capability.
If we look at the expression (1), we can conclude that not only the mean is playing a role in Cpk
estimation uncertainty. S is also an important parameter. Nevertheless, if we represent how σ
uncertainty is changing as n increases in a similar way than with the mean, the result is shown in
figure 2. In this case we are using Chi-Square to work out the upper bound of the confidence
interval for S. We will use the complete expression in the next section.

Looking at figure 2, we can conclude that the convergence of the estimation of sigma is achieved
before the one for the mean. That is the same of saying that the uncertainty of the mean is more
critical in terms of uncertainty due to sample size. This means, that we still have the same critical
value of 30 units as minimum, but we will use both confidence intervals, the one from the mean,
and the one for the standard deviation, to estimate Cpk.

2 Methodology

The reason why the traditional method is using the expression (1), which disregards the
uncertainty in the estimation of σ and μ, is that their estimation errors are considered negligible
when sample size is 30 or more. We have shown this idea in figures 1 and 2.
Then, the same logic tells us that when sample size is less than 30, we cannot consider that
uncertainties as negligible.
In the following lines, we are going to present the fundamentals to develop a method for the
estimation of Cpk when sample size is less than 30 individual measures.
When we do not know the standard deviation of the population, we have to use t-student
distribution for the estimation of confidence interval of the mean. The expression for this purpose
is the equation (2):

Nevertheless, we can use Z distribution if we consider the upper bound of the confidence interval
of σ (instead of S), which would be our worst case since the bigger the standard deviation, the
smaller the Cpk. We can see it in the opposite way, if we considered t-distribution in the
expression and the upper bound of σ, then, we would consider the uncertainty of not knowing
standard deviation of the population twice, which would not be correct.
Therefore, by using the following expressions (3) and (4) together, we will estimate upper bounds
(UB) and lower bounds (LB) for either the mean and the standard deviation from the sample.

As we have already justified before, we will only use the UB from the expression (4) as it is the
worst case. From the expression (3) we will get both the UB and LB for the mean.
For this method, we can use either the expression (2) or (3) to estimate the CI of the mean.
Although for n<30, the width of the CI from equation (3) is bigger than the one from (2) for the
same nominal coverage, both expressions will give us very similar results in practical terms.
Therefore, the estimation of Cpk when having less than 30 measures should be worked out using
the expression (5):




Cp index would be estimated using the same approach, but in that case, the estimation would be
much easier since the mean does not appear in Cp estimation. We could estimate potential
capability by using the expression (6):

2.1 Confidence Interval Estimation for Capability Indexes

If we look at the equation (5) it becomes obvious that this expression is indeed estimating the
lower bound of the Cpk, so we can write:

Selecting the minimum from the 4 options that are possible when the standard deviation is on the
upper bound, works well for CpkLB (taken from equation (4)) since it is giving us the lowest possible value for the closest specification limit without any contradiction with the actual capability definition from equation (1).
For the estimation of the upper bound, one can think of selecting the maximum when sigma is on
the lower bound which would give us the maximum distance. The problem is that by doing it, since it would give us the larger distance to the FARTHEST limit, it would clearly contradict Cpk definition and equation (1). So to estimate upper bound, we have to select the larger distance to the CLOSEST limit, and therefore not contradicting Cpk definition. The following expression could be an option to solve the problem for Cpk’s upper bound:

One can think in another possible expression, which would apparently give us the same result:

Equation (8) is not giving us the maximum value to the closest spec limit. Instead, it is giving us the minimum value to the farthest limit. It can be easily verified with an example, for instance, using ‘boobstrap’ techniques. Therefore, we use expression (9), since it is computing the maximum value to the closest spec limit, thus according to Cpk definition and equation (1).

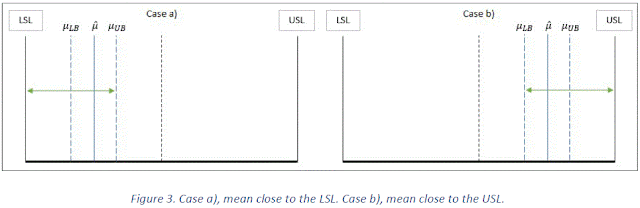
In Figure 3, we can see how equation (9) is computing the correct value for CpkUB. In the case a), μ is close to the LSL and μUB-LSL is selected. In the case b), μ is close to USL and USL-μLB is selected.

Equations (7) and (9) can be further simplified since:

Then:

Therefore:

Confidence Interval (CI) for Cpk is built on the confidence level (CL) from two parameters, μ and σ.
Therefore, the confidence level (CL), 1-α, for Cpk will have the following expression:

Since k=2 (2 parameters):

Where:
- α’ is the significance level from the desired confidence level for Cpk’s interval.
- α is to compute each of the CI of μ and σ. It is the α from equations (2), (3) and (4).
Therefore, if we want to compute the CI for Cpk using the typical α of 0.05 (5%), the resulting α’
will be 0.0975 (9.75%). Note that 0.0975 is approximately 10% that is one of the values
recommended by R. Fisher for fiducial intervals and hypothesis tests, which has been widely used since then. On the other hand, if we want to use α’=0.05, then to compute CI for μ and σ, we have to obtain α from equation (12):

If α’=0.05, then:

This relationship can be also verified for the other recommended value by Fisher, 1%. From (12):

If α << 2, then 2-α≈2, therefore:

Expression (14) will be accomplished for most of the cases, where values recommended by R.
Fisher and usually applied are included (0.1, 0.05 and 0.01).

And for Cp we have to generalize expression (6) to compute both confidence intervals as follows:

3 Synthesis

To use confidence interval for capability indexes we have to use the following expressions:
- For Cpk:

Note that we could use equation (3) instead of (2) since they give us very similar results and there would not be any significant difference between the two in practical terms for most of the cases.

- For Cp:

Note that equation (17) is the synthesis of equations (15) and (16). Although a similar synthesis is
possible for Cpk, we have considered that for clarity reasons it is better to express them using two separate equations, which are the expressions (10) and (11).
Two different approaches are possible when dealing with n<30; one is to estimate confidence
intervals using all the expressions above listed, and the other one is to use only LB expressions for either Cpk or Cp, which are the worst possible cases for a given α.
With the confidence interval one can also decide if taking more samples could be worth it based
on the width of the confidence interval.

4 Application of the method

To facilitate the practical application of the method, an Excel file prepared by the author of this blog is available through sending a request to the following e-mail address:

rasanmar18@gmail.com