YouTube video:
https://youtu.be/ZbJj9whKXco
Method Explanation step by step
INTRODUCTION.-
The main objective is to establish a graphical method to see in a chart when we have enough samples to have a good estimation of any distribution parameter.
Within the next slides we are going to see how parameters behave as we increase sample size over the time.
Each time an additional individual is measured/evaluated the estimation is recalculated again and the new point is shown on the chart including all the individual observations to that moment which have been taken out of the population.
Normal distribution
Look at the graph on the next page.
Each point of the graph represents the estimation of the mean of all individuals we have already taken from the population at that very moment.
Sample size is increasing over the time and the estimation of the mean starts to be stable around n=45->50. These points belongs to a normal distribution with mean=1 and sigma=1, and have been generated using Microsoft Excel. Excel file attached to this presentation on the last slide.
We can conclude that we could generate this graph while we increase the sample by taking more individuals from the population and would stop taking more when the estimation becomes stable, in this first case, around n=50.
Something similar happens with the standard deviation, but in this case we would need a sample a bit larger, n=60->70.
However the graph itself will tell us when to stop taking more samples!!!
Normal distribution with mean = 1 sigma = 1
In this case we would estimate mean ≈ 1,13 when the population has a mean of 1.
Quite good estimation, don’t you think?
We would need a sample of n=40->50
If we use a sample of 30 we would estimate mean = 1,39
Normal distribution with mean = 1 sigma = 1
In this case we would estimate sigma ≈ 1,03 when the population has a sigma of 1.
Quite good estimation as well, don’t you think?
If we use a sample of 30 we would estimate sigma = 1,23
Normal distribution with mean = 1 sigma = 3
In this case we would estimate mean ≈ 0,9 when the population has a mean of 1.
Quite good estimation, don’t you think?
We would need a sample of n=70->80
If we use a sample of 30 we would estimate mean = 1,65
Normal distribution with mean = 1 sigma = 3
In this case we would estimate sigma ≈ 2,97 when the population has a sigma of 3.
Quite good estimation as well, don’t you think?
If we use a sample of 30 we would estimate sigma = 2,50
It seems that estimation of mean is quite sensitive to value of sigma. Let’s increase sigma to confirm our suspicions.
Normal distribution with mean = 1 sigma = 6
In this case we would estimate mean ≈ 0,9 when the population has a mean of 1.
Quite good estimation, don’t you think?
We would need a sample of n=110->120
If we use a sample of 30 we would estimate mean = 1,65
Confirmed! Sample size for the estimation of mean is sensitive to the value of sigma!
Normal distribution with mean = 1 sigma = 6
In this case we would estimate sigma ≈ 6,1 when the population has a sigma of 6.
Quite good estimation as well, don’t you think?
If we use a sample of 30 we would estimate sigma = 6,2
Let’s try with another distribution also widely used in 6 Sigma Projects.
Poisson distribution
Look at the graphs on the next pages.
Each point of the graph represents the estimation of Defects per Unit (DPU) which is the unique parameter for a Poisson distribution. All units been have taken from the population.
This distribution has been also generated using Microsoft Excel.
Poisson distribution Lambda (dpu) = 1
In this case we would estimate dpu ≈ 1 when the population has a dpu of 1.
It is the best estimation we could get!
We would need around 330 samples.
If we use a sample of 100 we would estimate dpu = 0,96. Not too bad.
Poisson distribution Lambda (dpu) = 3
In this case we would estimate dpu ≈ 3 when the population has a dpu of 3.
It is the best estimation we could get
We would need around 110 – 120 samples.
If we use a sample of 100 we would estimate dpu = 2,95. Not too bad.
Again it seems that n for dpu estimation is sensitive to the value of dpu itself.
Poisson distribution Lambda (dpu) = 9
In this case we would estimate dpu ≈ 9,1 when the population has a dpu of 9.
Quite good estimation, don’t you think?
We would need around 70 – 80 samples.
If we use a sample of 100 we would estimate dpu = 9,17. Not too bad as well.
Confirmed! We need less sample size as dpu gets bigger.
Let’s try with another distribution also widely used in 6 Sigma Projects.
Binomial distribution
Look at the graphs on the next pages.
Each point of the graph represents the estimation of Proportion of defectives (p) which is the unique parameter for a Binomial distribution. All units have been taken from the population.
This distribution has been also generated using Microsoft Excel.
Binomial distribution p=0,5
In this case we would estimate p ≈ 0,49 when the population has a p of 0,5.
Quite good estimation, don’t you think?
We would need around 180-190 samples.
If we use a sample of 100 we would estimate dpu = 0,47. Not too bad.
n=1 on the graph means each point represents an increase of n=1 in the total sample size.
Binomial distribution p=0,1
In this case we would estimate p ≈ 0,1 when the population has a p of 0,1.
It is the best estimation we can get!
We would need around 330 samples.
If we use a sample size of 100 we would estimate p = 0,13.
It seems that sample size for the estimation of p is sensitive to the value of p itself.
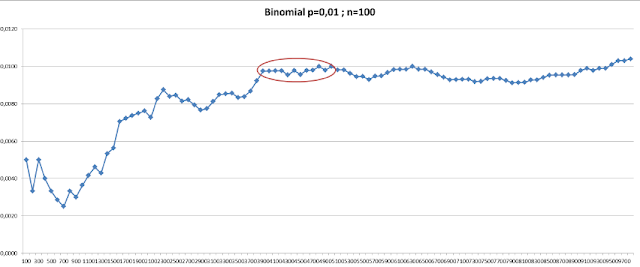
Binomial distribution p=0,01 ; n=100
We have had to use samples in subgroups of 100 individuals for this simulation.
In this case we would estimate p ≈ 0,01 when the population has a p of 0,01.
It is the best estimation we can get!
We would need around 4000 samples!!!
If we use a sample size of 100 we would estimate p = 0,005. A lot of error in the estimation.
It is obvious sample size for the estimation of p is very sensitive to the value of p.
CONCLUSIONS
-This graphical method used along with empirical rules is very useful and increases the quality of estimation of parameters for any statistical distribution.
-It gives us the best estimation using the correct sample size. Sometimes it means using less resources than with the use only of practical rules.
-Sample size for the estimation of mean is sensitive to the value of sigma! As sigma becomes bigger the sample size for mean estimation increases as well.
-In the Poisson distribution we need less sample size as dpu gets bigger.
-Binomial: sample size for the estimation of p is very sensitive to the value of p. As p becomes smaller, sample size needed for its estimation becomes bigger.